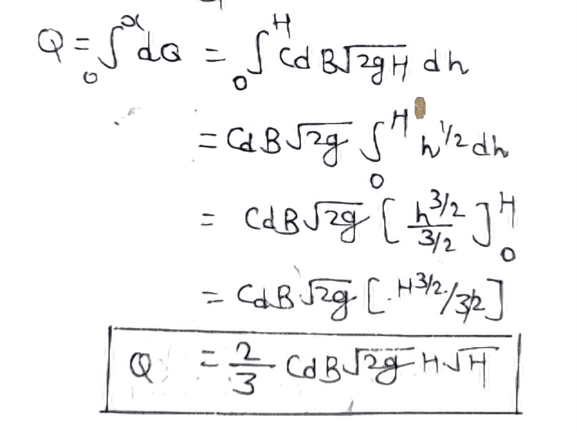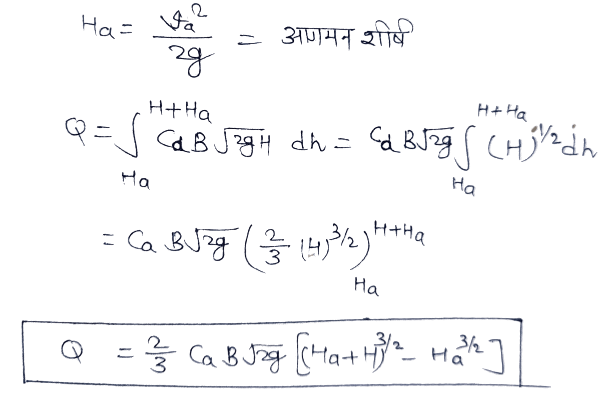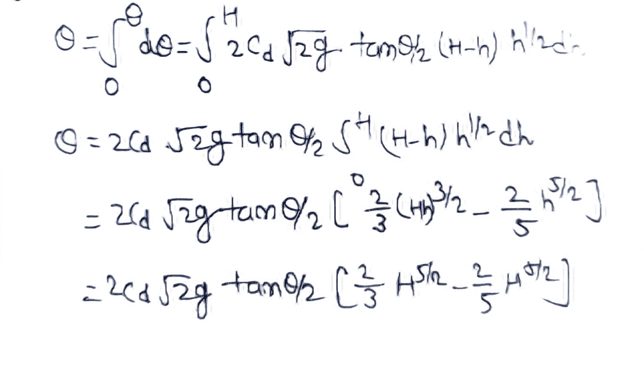Rectangular Notch or Shesporested Weir Formula

Due to the contraction at the edge of the notch or weir, the value of actual discharge is theoretically reduced. Derivation of Notch and Weir formula by immersion of velocity.

Let the discharge constant be Cd 

{tocify} $title={Table of Contents}

(i) When the arrival velocity is zero 

Because the thickness of the strip is very low. Hence the velocity of the fluid at each point due to the head can be taken as √2gh. 

Strip in change 

Cd x B.dh x √2gh ............(i)

The entire area (BxH) of the flow can be bounded by many such strips. The sum of the discharge from all these strips is equal to the total discharge from the bottom or wiper. 

Therefore, integrating equation (i), the value of h varies from h = 0 to h = H).  

(ii) When the arrival velocity is Va 

In this case, the fluid reaches the weir with a velocity Va, thus the top H flowing through the notch or weir will be (H + V²a/2g) or (H +Ha).

And in the first case where H = 0, the value of the vertex will be V²a/2g or Ha. Since the arrival velocity is the same everywhere, the limits of the integral of equation (i) will be Ha and (H+Ha).

Ha = V²a/2g = arrival top

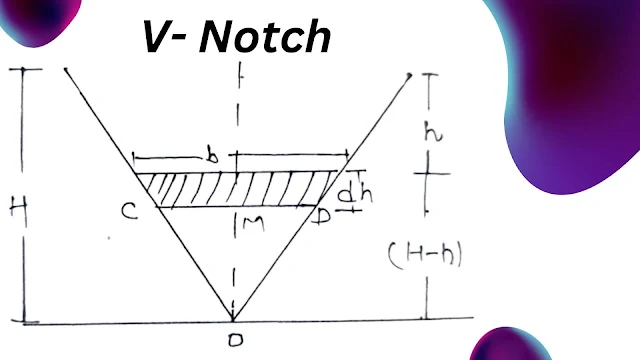
Rectangular V Notch

The immersion of the liquid is measured more smoothly by the V notch. Because for a given immersion the apex will be higher in a V notch than in a rectangular notch. 

(i) When the arrival velocity is zero 

Let there be a vertical strip of very small thickness dh at a depth h from the free surface of the liquid, the width of this strip ∆OMD.

tan Q/2 = MD/MO = b/2/(H-h)

b = 2(H-h) tan Q/2

Area of ​​strip = b x dh = 2x(H-h) tanQ/2 

Flow Velocity of strip = 2√2gh 

Immersion in strip 

dQ = Cd x Area of ​​strip x flow Velocity of strip 

dQ = Cd x 2(H-h) tanQ/2 x 2√2gh .........(i)

Multiple strips can be considered in the entire V notch, integrating equation (i) for the entire immersion from the notch.

Q = 90° for right angle notch 

Q/2 = 45° 

tanQ/2 = tant 45°

Immersion for right angle notch from equation (2).

(ii) When the arrival velocity is Va

In this case also the arrival velocity is Va so due to this the top.

Ha = V²a/2g

 V² = 2gHa 

If the vertex acts parallel to the V notch. It is related to equation (i) Limits of integration-